Extracting measures of term premia from the term structure of interest rates is important to evaluate the response of financial markets to monetary and fiscal policy. The standard literature achieves the decomposition of yields by estimating a common factor structure for yields and excess returns. This column introduces a model in which yields are drifting, sharing a common stochastic trend driven by the drift in short-term (monetary policy) rates, and excess returns are stationary, as the compensation for risk is driven by the cycles in yields. The model produces much better forecasts of the dynamics of US rates at all maturities and leads to a very different measurement of term premia.
Although, as illustrated by Rogoff et al. (2022), there is evidence that over a 700-year horizon yields are stationary, the data tell us that over an horizon of 50 years bond yields are drifting, while returns obtained by holding for one-quarter bonds at maturity in excess of the return of the three-month rates are stationary. Figures 1 and 2 illustrate this evidence for US data.
Figure 1


Note: Quarterly observations on the time-series of (annualised) yields from the 3-month to the 15-year maturity. We use the same colour palette for all maturities (blue). Darkest blue indicates the highest maturity, i.e., 15 years
Figure 2
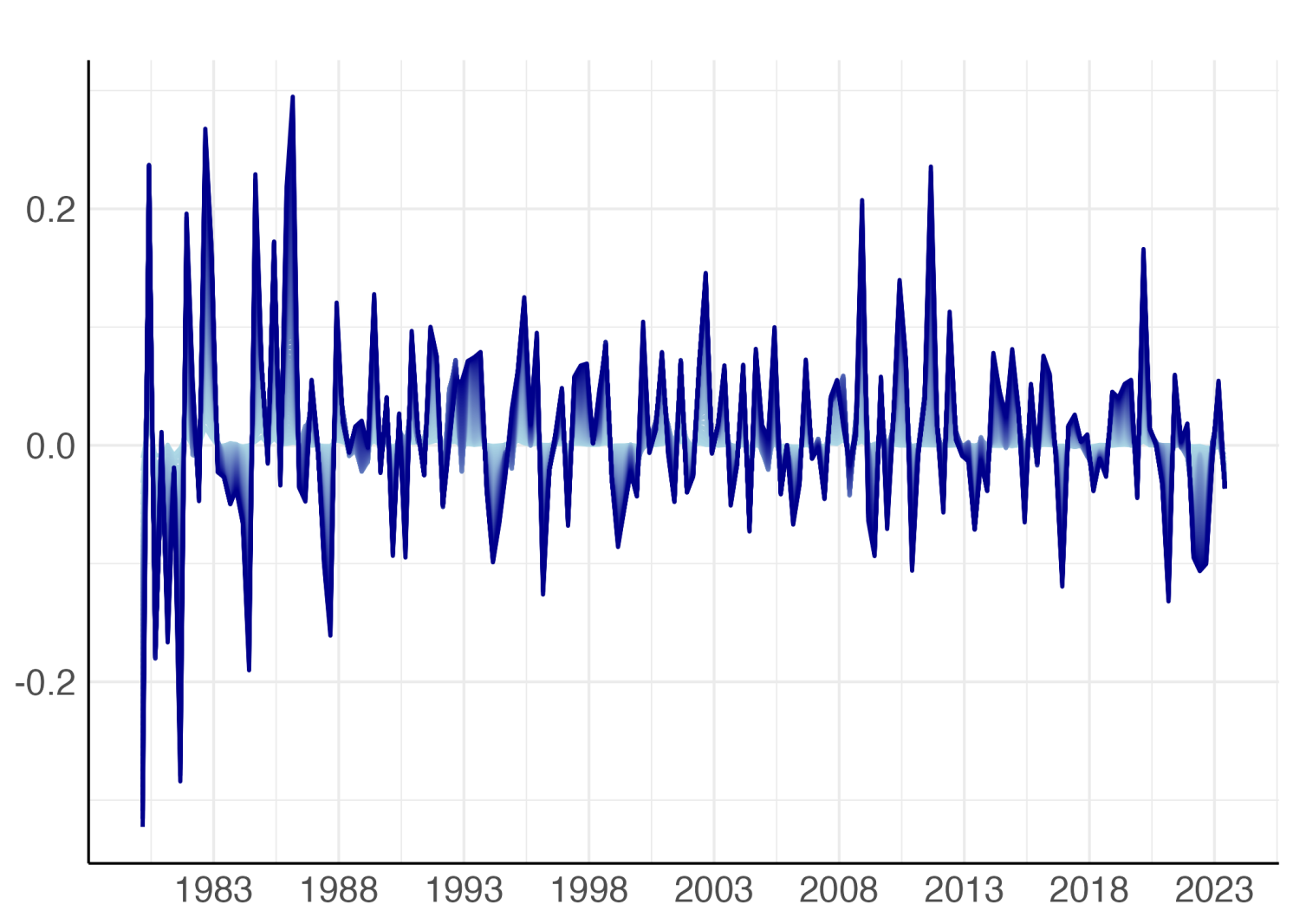
Note: Quarterly observations on the time series of 1-quarter holding period returns for bonds at maturities between 5 and 15 years in excess of the return on three-month Treasury Bills
The dynamics of nominal government bond yields at different maturities plays a central role in shaping the response of the real economy to monetary and fiscal policy interventions.
Yields can be decomposed into two unobservable components: the sequence of expected one-period rates and the term-premia (Campbell 1991, Duffee 2002). The first component reflects the future expected path of monetary policy rates, while the second reflects both macro fundamentals, including the prospects for growth, inflation and government debt dynamics, and investors’ attitude toward risk.
Policymakers are fully aware that the market-based financing conditions that matter for the control of the business cycle and inflation depend on both components of yields. Fluctuations in term premia are considered as important as the market perception of the future path of interest rates (Schnabel 2022), and they are also used to evaluate the macroeconomic implications of monetary policy (Schnabel 2023).
Term structure models are helpful in that they allow the identification of the two components by forecasting the expected path of interest rates and by imposing consistency with no-arbitrage restrictions for the derived term premia at different maturities.
In standard affine macro term structure (AMTS) models, a few factors, modelled by a vector autoregressive process, are the common drivers of the dynamics of both the expected path of future one-period rates and the term premia. As yields drift, factors exhibit a high level of persistence. When these factors are modelled using a vector autoregression (VAR), the forecast of future one-period rates gradually converges to the mean of the sample used for estimation.
Standard AMTS models tend to generate term premia that are a-cyclical and parallel to the secular trend in yields. These features of the term-premia are a byproduct of the specification strategy for the dynamics of yields and excess returns that adopts a common autoregressive factor structure for them.
In a recent paper (Favero and Fernandez-Fuertes 2023), we propose a new AMTS model in which yields drift, sharing a common stochastic trend driven by the drift in short-term (monetary policy) rates, and excess returns are stationary as the compensation for risk depends on the cycle in yields.
The objective of our contribution is to build an affine no-arbitrage term structure model consistent with the evidence from the data that yields are non-stationary and driven by a common trend, while excess returns are stationary.
Following Favero et al. (2022), short-term rates are decomposed in a trend component and a cycle component. The trend component is driven by the very long-run forecast of the central bank for real short-term rates and by the response of monetary policy to the very long-run forecast for inflation. The very long-run forecast for the real rates is labelled in the literature as the natural rate of interest. The natural rate is modelled as function of the equilibrium growth rate of output in the economy and the age structure of population, a time-varying determinant of household preferences.
We provide statistical evidence that these variables capture successfully the trend in one-period rates and that the trend in yields at all maturities is successfully modelled by the average of the trend in one-period rates over the residual life of the different bonds.
Given the availability of long-run forecasts for the growth rate of the economy, the age structure of the population, and long-term expected inflation, the current and future trend component of the short-term rates are constructed.
A factor model is then built for the cyclical components of yields, where the dynamics of holding period excess returns and term-premia is consistent with no-arbitrage restrictions.
We keep a VAR specification for the identified factors, but it is a VAR on stationary variables. Predictions for short-term rates at any future dates are then derived by combining the predictions for the trends (not based on the VAR for factors, and therefore forward-looking) and the predictions for the cyclical components (based on the VAR for factors, and therefore backward-looking). Bonds at any maturities are then priced via pricing equations that impose no-arbitrage restrictions. Term premia are derived as the difference between bond yields obtained when the price of risk is estimated in the affine specification and when the price of risk is restricted to zero.
Bond yields are non-stationary, but their trend is the average trend of short-term rates over the maturities of the bond, and term premia are driven by the stationary state variables.
The specification strategy dominates standard models in term of forecasting performance for returns and yields at any maturity and leads to a very different measurement of term premia.
Figure 3 illustrate the point by reporting long-term forecasts for the 3-month and the 10-year rate made by simulating out-of-sample a standard model ATSM (Adrian et al. 2013) and our model FF from 2008 onwards. While the standard model predicts mean reversion of yields our model generates different forecasts driven by the demographic and productivity determinants of the trends in yields.
Figure 3
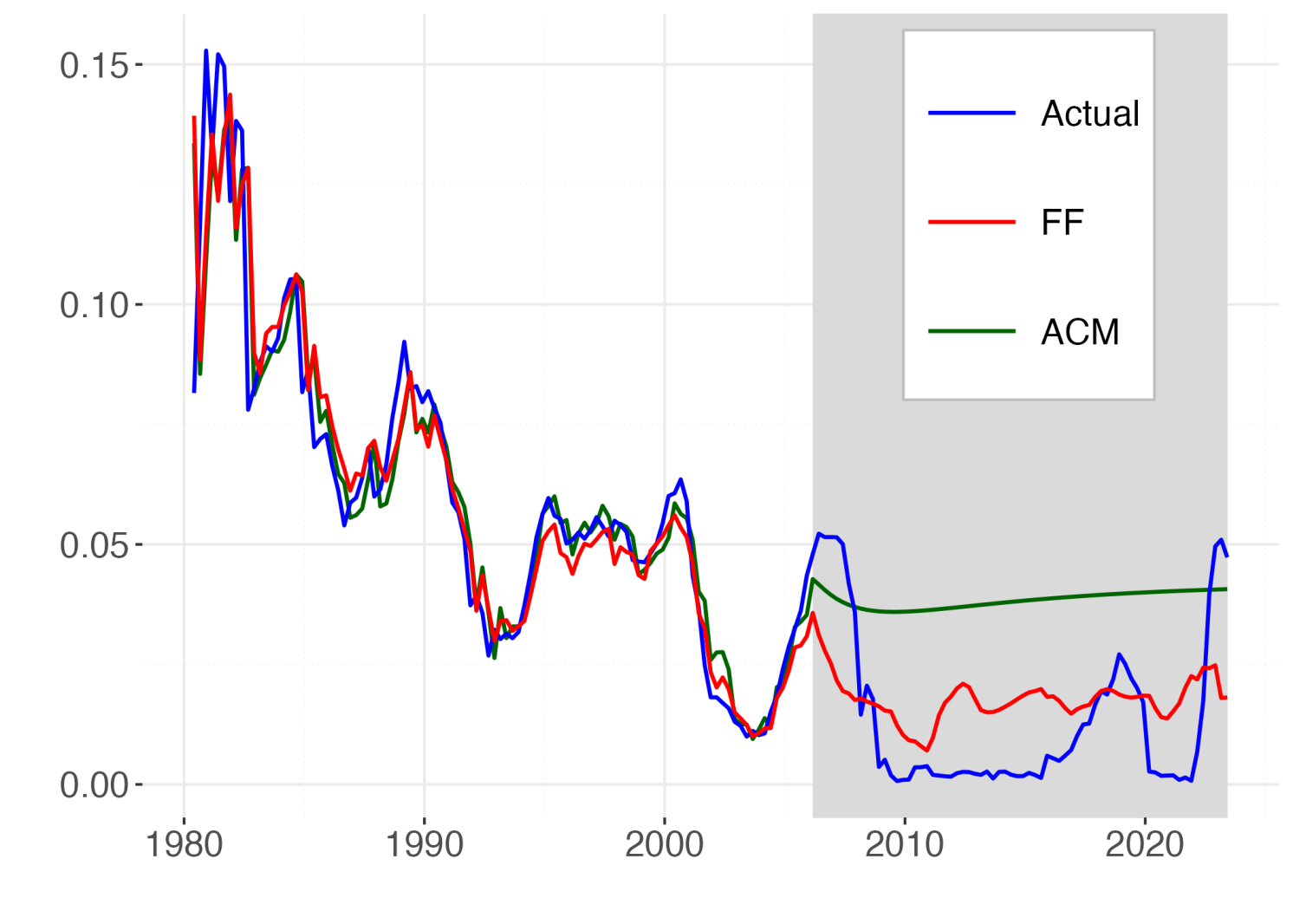
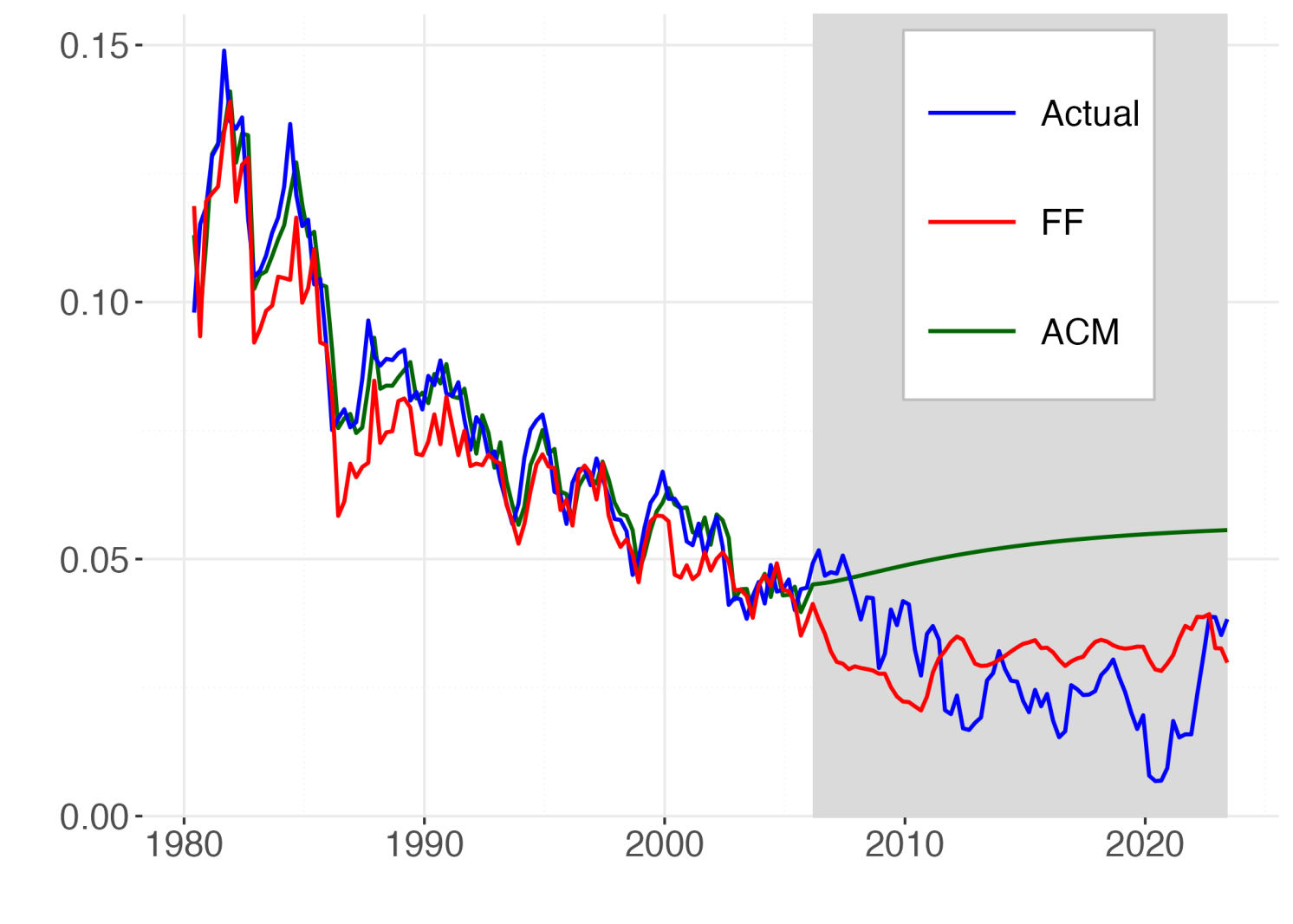
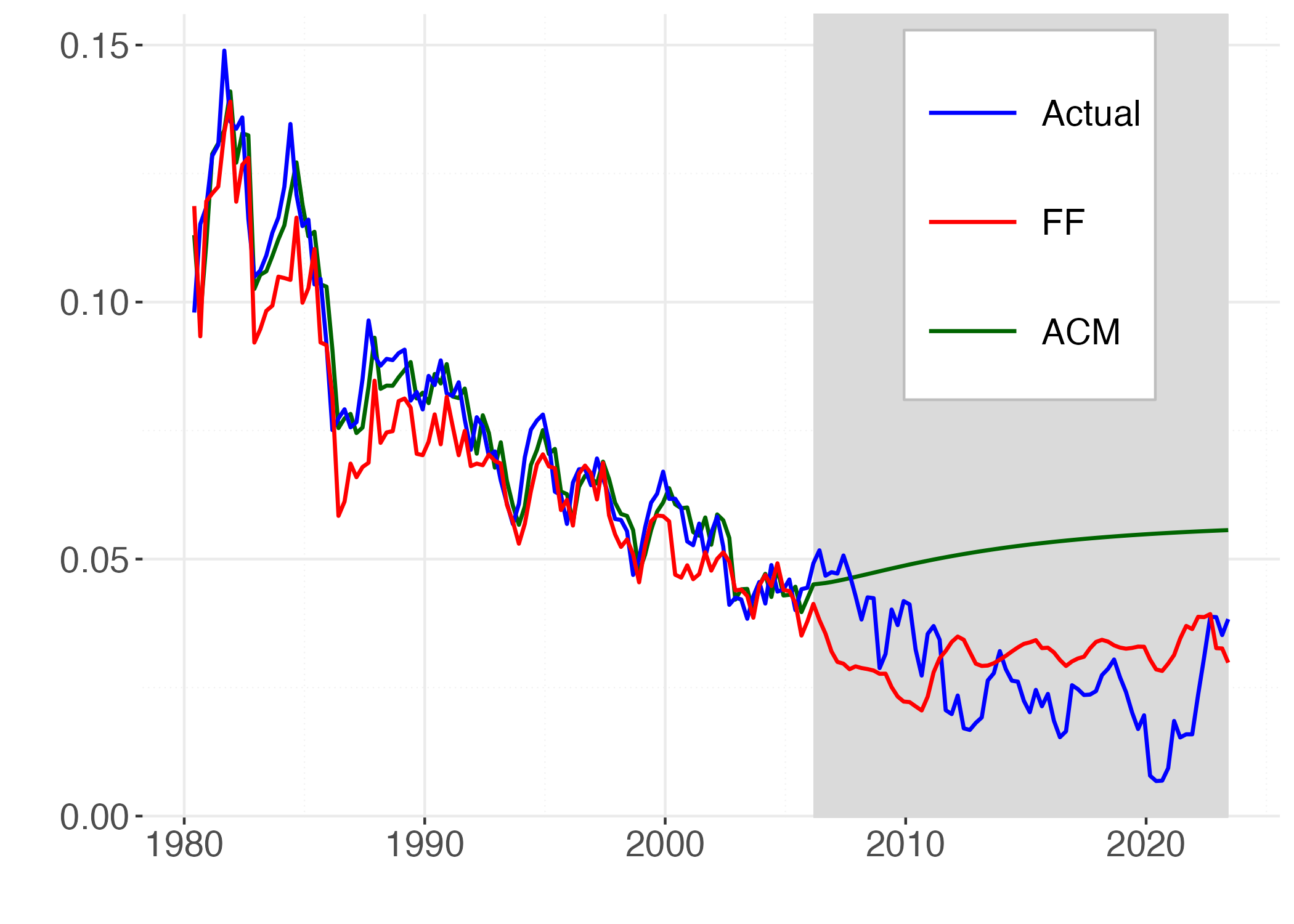
Note: This graph reports the fitted (1980Q1:2005Q4) and the forecasted (2006Q1:2023Q2) time series of 1Y and 10Y yields given by the standard ACM model (green) and our model (red) against the actual values (blue). The shaded area indicates the selected out-of-sample period.
The different forecasts of the sequence of expected monetary policy rates from the two different models generate different measures of the term premia, reported in Figure 4.
Figure 4

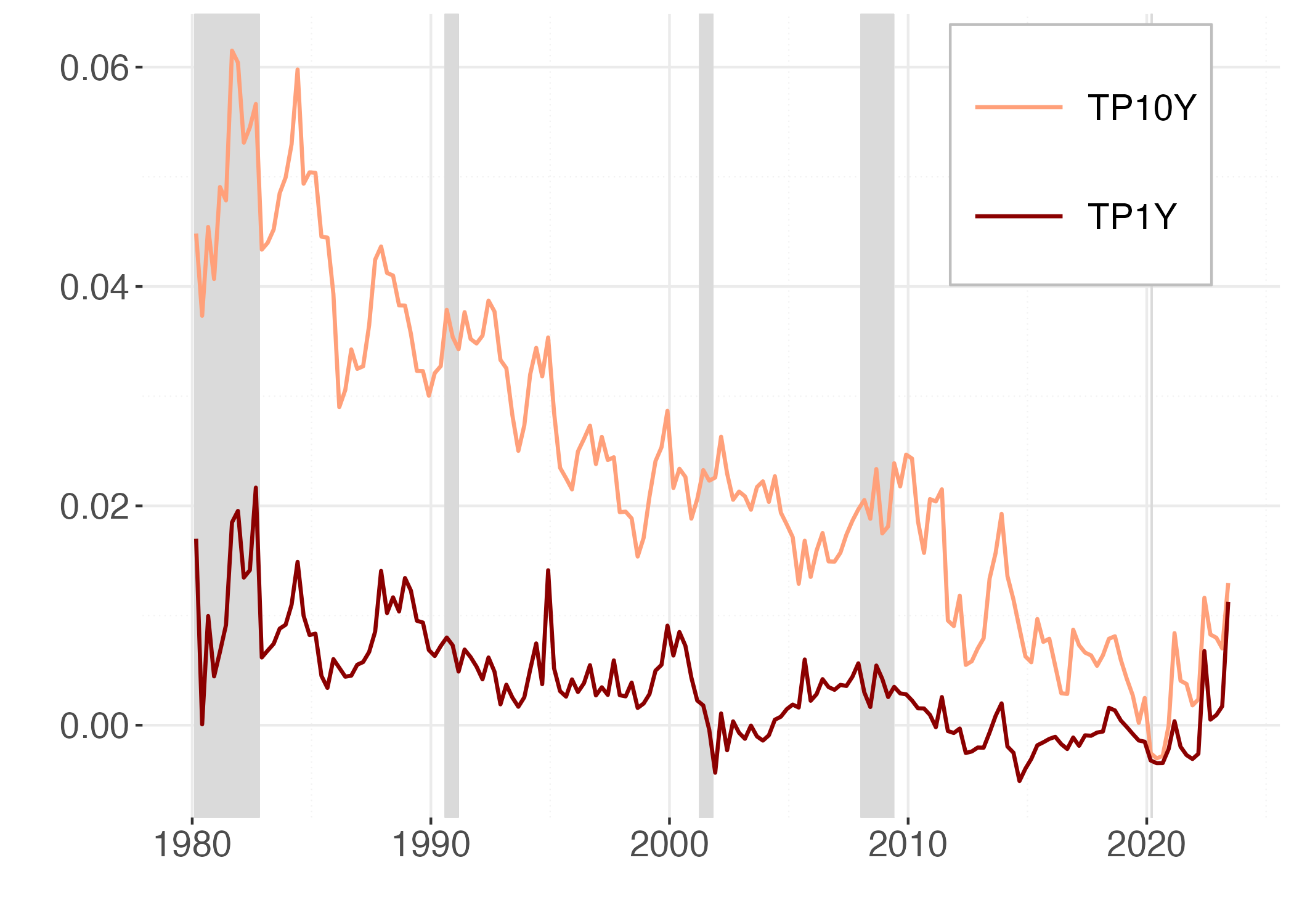
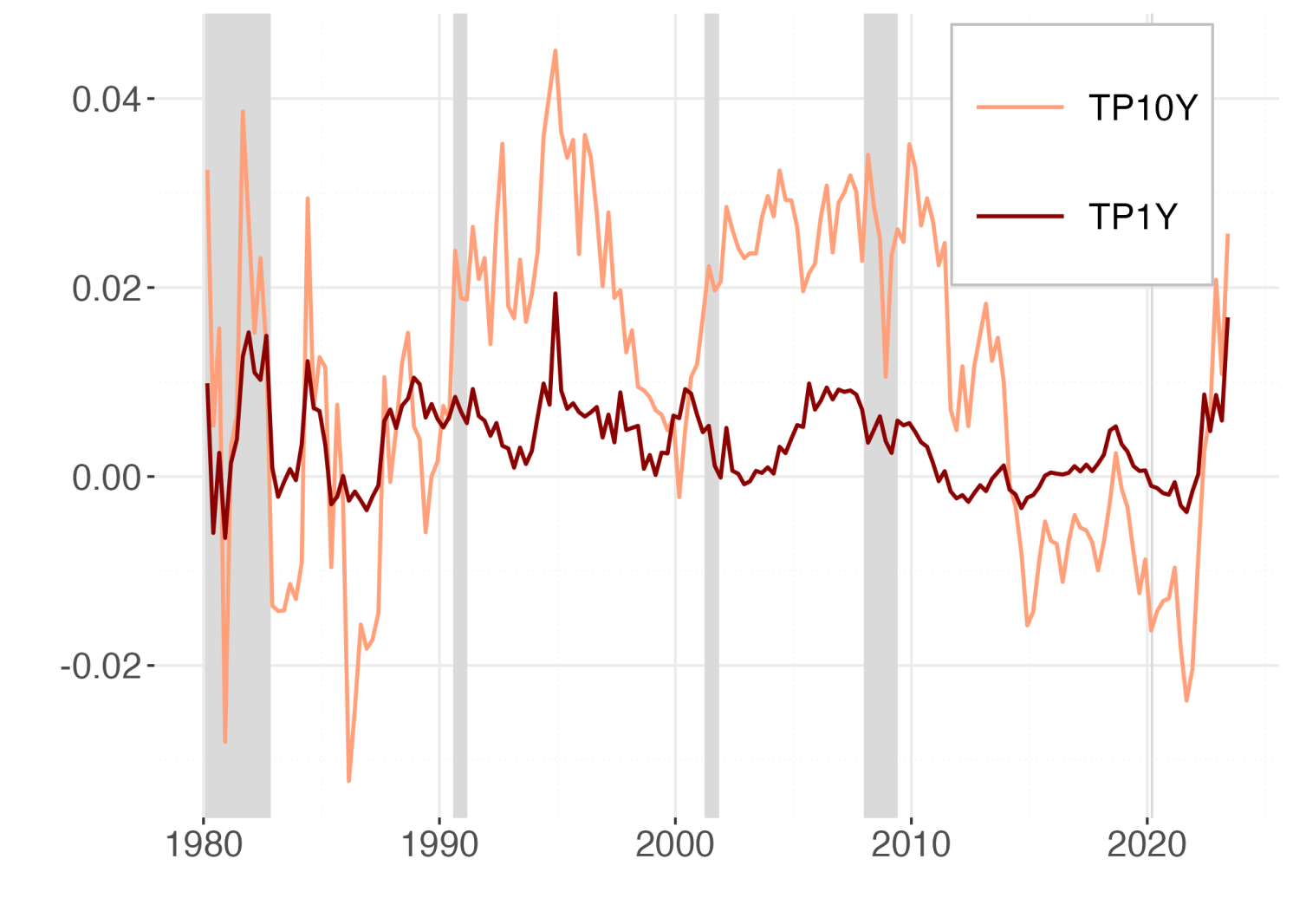
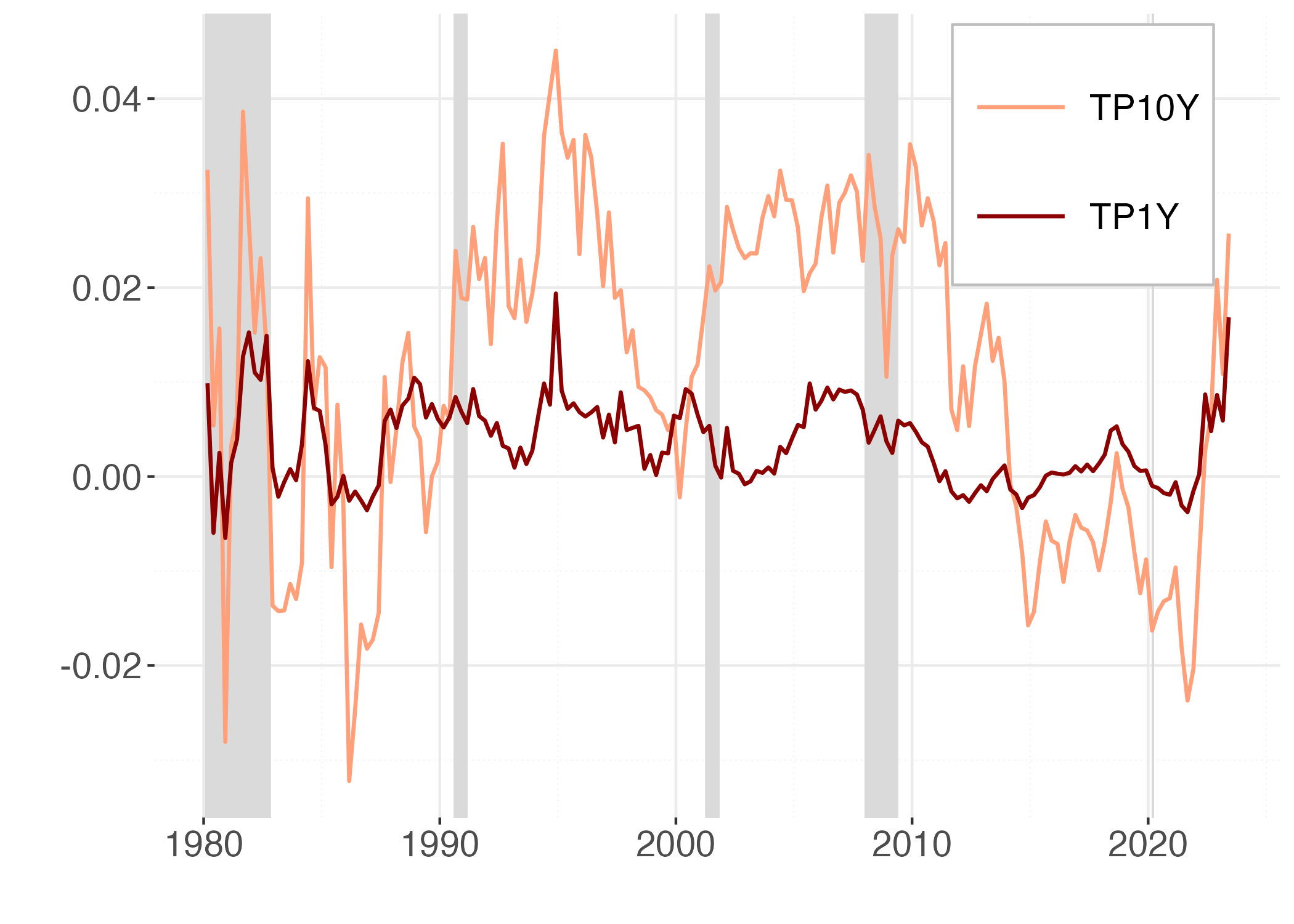
Note: This figure reports the 1Y (red) and 10Y (orange) term premia in the ACM and the FF models. Shaded areas coincide with recession periods.
The 10-year term premium suggested by the conventional model exhibits a noticeable trend, in contrast to the model that uses the trend-cycle decomposition of yields, where a cyclicality in term premia emerges. The a-cyclicality of term premia estimated by standard ATS models and their parallelism to the secular trend in long-term interest rates has been already noted by Bauer et al. (2014) in commenting on the estimates provided by Wright (2011). Bauer et al. (2014) attribute the acyclicality to small sample bias caused by the very high persistence in the VAR model for factors; they show that biased-adjusted estimates produce instead countercyclical term premia. In fact, adjusting for small sample bias produces estimates that are much closer to the unit root, preventing the sequence of predicted one-period rate from converging to a biased estimate of their level.
Our approach is different in that the trend in one-period rate is captured by the long-term drivers, and factors are then extracted from the deviations of yields from their drift explained by productivity demographics and long-term inflation forecasts. Our VAR for factors is much less persistent and the parameters estimates do not require a small sample adjustment. As a result, the sequence of predicted one-period rates features much smaller forecast errors than the equivalent in standard ATS models and also our estimates of the term premia show some counter-cyclical behaviour visible in Figure 4, where the NBER recessions are highlighted by shaded areas. This evidence is in line with the empirical and theoretical research that has found support for countercyclical risk premia, including, among many others, Campbell and Shiller (1987), Cochrane-Piazzesi (2005), Campbell and Cochrane (1999), and Wachter (2006).
Source : VOXeu





